平衡树
- 我自己的复习就开始从平衡树开始吧
- 这是我最早咕的一个知识点,现在来看,我那时菜得竟然连都看不懂,
特点:
- 优点:
- 最常用最好写的平衡树,在考场上如果可以实现,打起来是最快的。
- 不是很慢,甚至可以说挺快的。
- 缺点:
- 通用性和扩展性不如
- 优点:
算法:简而言之就是一个二叉搜索树+一个堆。
众所周知,堆是一个完全二叉树,所以我们只要在一个中的每一个结点创造出一个附属值(在堆中的优先级),然后再用堆化为一个接近完全二叉树的(还要满足的性质下)。如果要插入一个数,用
rand进行优先级赋值。然后加入到树中去(的加入方法,不是堆的加入方法,否则不满足)。然后就是一个堆的上浮过程了,根据实际情况进行相连的两个节点的左旋和右旋。
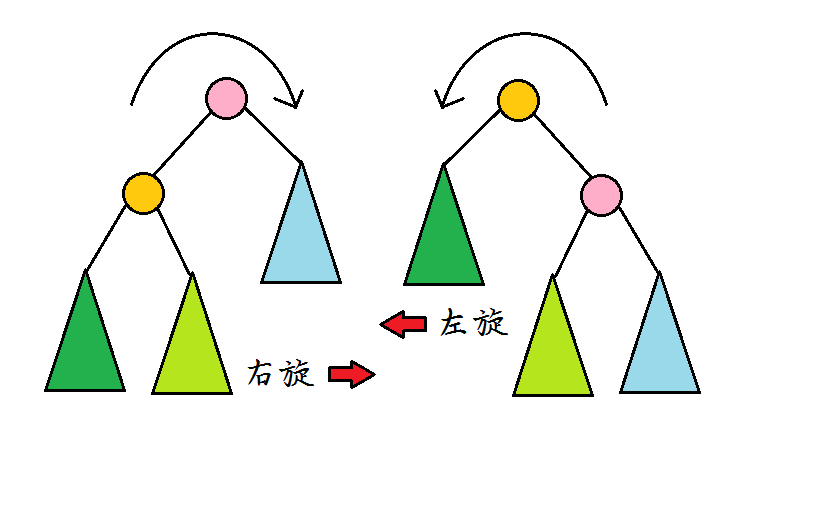
旋转如果看不懂,就再看看下面的代码帮助理解。其实就是在旋转中交换儿子,左旋和右旋的交换都是固定的。不需要考虑多种情况。
再然后就没有什么了,更多的功能按照自己需要的加。
每个树节点几个属性(或者说你要开几个不同的数组),
l[]左二子,r[]右儿子,sum[]这个数有几个(因为你可能会插入多个一样的数),rank[]优先值,val[]这个节点的值,size以这个节点为根的子树有多少个结点。
例题:普通平衡树
- 模板题,直接打即可,插入和删除都和线段树比较类似。
#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std;
const int MAXN=100005;
int n;
struct treap{
int l[MAXN],r[MAXN],val[MAXN],rank[MAXN],size[MAXN],sum[MAXN];
int sz,ans,rt;
inline void pushup(int x){
size[x]=size[l[x]]+size[r[x]]+sum[x];
}
inline void lrotate(int &k){
int t=r[k];
r[k]=l[t];
l[t]=k;
size[t]=size[k];
pushup(k);
k=t;
}
inline void rrotate(int &k){
int t=l[k];
l[k]=r[t];
r[t]=k;
size[t]=size[k];
pushup(k);
k=t;
}
void insert (int &k,int x){
if (!k){
sz++;
k=sz;
size[k]=1;
sum[k]=1;
val[k]=x;
rank[k]=rand();
return;
}
size[k]++;
if (val[k]==x){
sum[k]++;
}
else if (val[k]<x){
insert (r[k],x);
if (rank[r[k]]<rank[k])
lrotate(k);
}
else {
insert (l[k],x);
if (rank[l[k]]<rank[k])
rrotate(k);
}
}
void del(int &k,int x){
if (!k) return;
if (val[k]==x){
if (sum[k]>1){
sum[k]--;
size[k]--;
return;
}
if (l[k]==0||r[k]==0){
k=l[k]+r[k];
}
else if (rank[l[k]]<rank[r[k]]){
rrotate(k);
del(k,x);
}
else{
lrotate(k);
del(k,x);
}
}
else if (val[k]<x){
size[k]--;
del(r[k],x);
}
else {
size[k]--;
del(l[k],x);
}
}
int queryrank(int k,int x){
if (!k) return 0;
if (val[k]==x){
return size[l[k]]+1;
}
else if (x>val[k]){
return size[l[k]]+sum[k]+queryrank(r[k],x);
}
else return queryrank(l[k],x);
}
int querynum(int k,int x){
if(!k) return 0;
if(x<=size[l[k]]) return querynum(l[k],x);
else if(x>size[l[k]]+sum[k])
return querynum(r[k],x-size[l[k]]-sum[k]);
else return val[k];
}
void querypre(int k,int x){
if(!k) return ;
if(val[k]<x) ans=k,querypre(r[k],x);
else querypre(l[k],x);
}
void querysub(int k,int x){
if(!k) return;
if(val[k]>x) ans=k,querysub(l[k],x);
else querysub(r[k],x);
}
}T;
int main(){
scanf("%d",&n);
int opt,x;
for(int i=1;i<=n;i++){
scanf("%d%d",&opt,&x);
if(opt==1)T.insert(T.rt,x);
else if(opt==2)T.del(T.rt,x);
else if(opt==3){
printf("%d\n",T.queryrank(T.rt,x));
}
else if(opt==4){
printf("%d\n",T.querynum(T.rt,x));
}
else if(opt==5){
T.ans=0;
T.querypre(T.rt,x);
printf("%d\n",T.val[T.ans]);
}
else if(opt==6){
T.ans=0;
T.querysub(T.rt,x);
printf("%d\n",T.val[T.ans]);
}
}
return 0;
}- 优化:
<cstdlib>的rand()有点慢,所以可以直接手写一个:
inline int rand ( ) {
static int seed = 233;//seed可以随便取
return seed = ( int ) seed * 482711LL % 2147483647;
}非旋
这个一般来说有点慢,但是可以让树可持久化。
可持久化就是:
可持久化数据结构(Persistent data structure)是一种在发生改变时,会保存之前的版本的数据结构。这是一种不可变的数据结构,对数据进行操作时,不会在原数据上进行更新改变,而是会生成另一个新的发生改变了的新数据。
所以这不应该很耗空间吗??
不常用,暂时不学。
这个 相比 来说更全能一点,除了可能代码会
又臭又长(好吧,其实并没有)。- 感觉更加优雅一些,因为用其他冗余的东西来平衡,只是单纯的左旋和右旋。
- 优点:和 差不多,比 扩展性更高
- 缺点:比 打起来慢一点,但是一般平衡树的题直接用它就可以了,万一 写到一半发现只能用 就比较尴尬。
基本操作
- 更新子树结点数量
size:
inline void UDsize(int x){
size[x]=size[son[x][0]]+size[son[x][1]]+cnt[x];
return;
}- 左儿子 右儿子:
inline bool lrson(int x){
return x==son[fa[x]][1];
}- 删除结点:
inline void clear(int x)[
size[x]=son[x][0]=son[x][1]=cnt[x]=val[x]=fa[x]=0;
return;
]- 旋转
(竟然不用分左右):用手模拟一遍就可以知道怎么旋转了
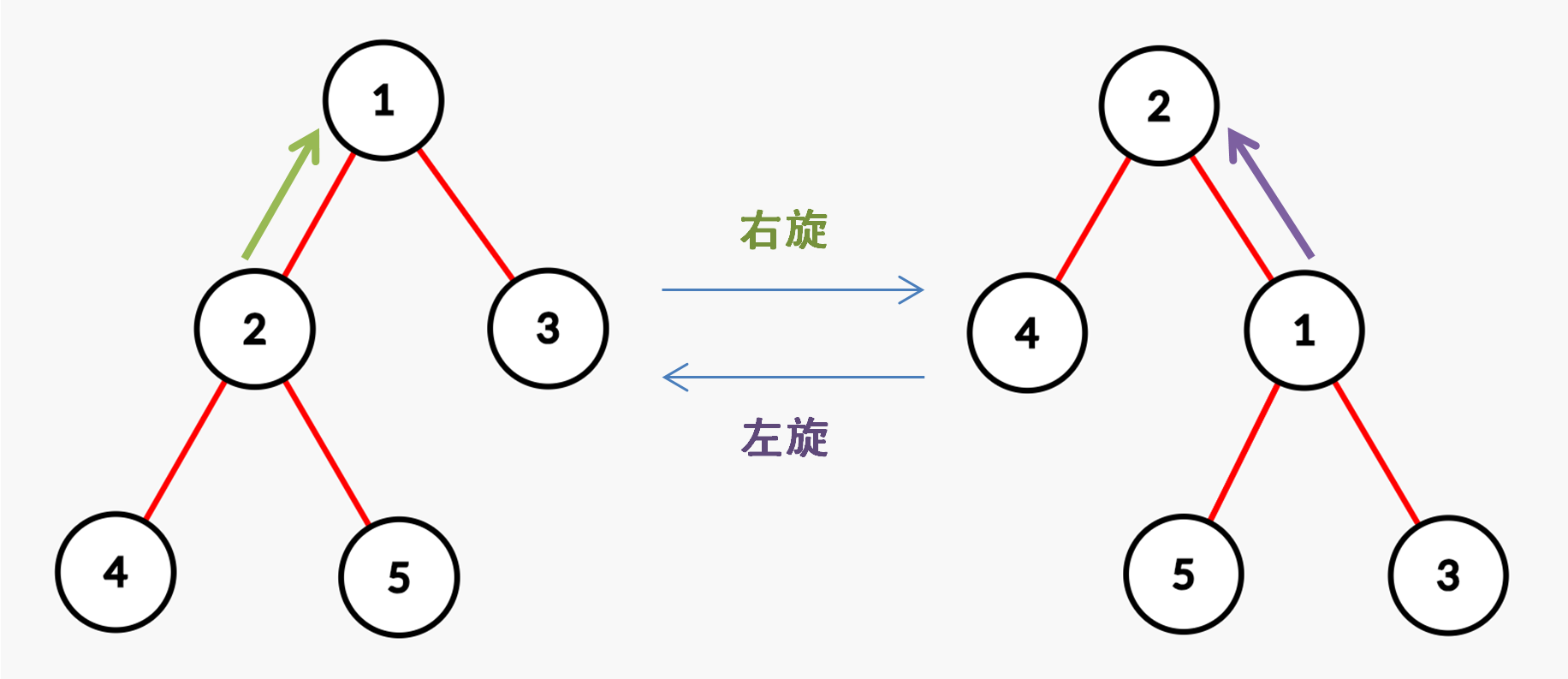
Splay旋转
inline void rotate(int x) {
int y = fa[x], z = fa[y], sonk = lrson(x);
son[y][sonk] = son[x][sonk ^ 1];
fa[ch[x][sonk ^ 1]] = y;
son[x][sonk ^ 1] = y;
fa[y] = x;
fa[x] = z;
if (z) son[z][y == son[z][1]] = x;
UPsize(y);
UPsize(x);
return;
}- 伸展:直接引用 OI-Wiki 的例子
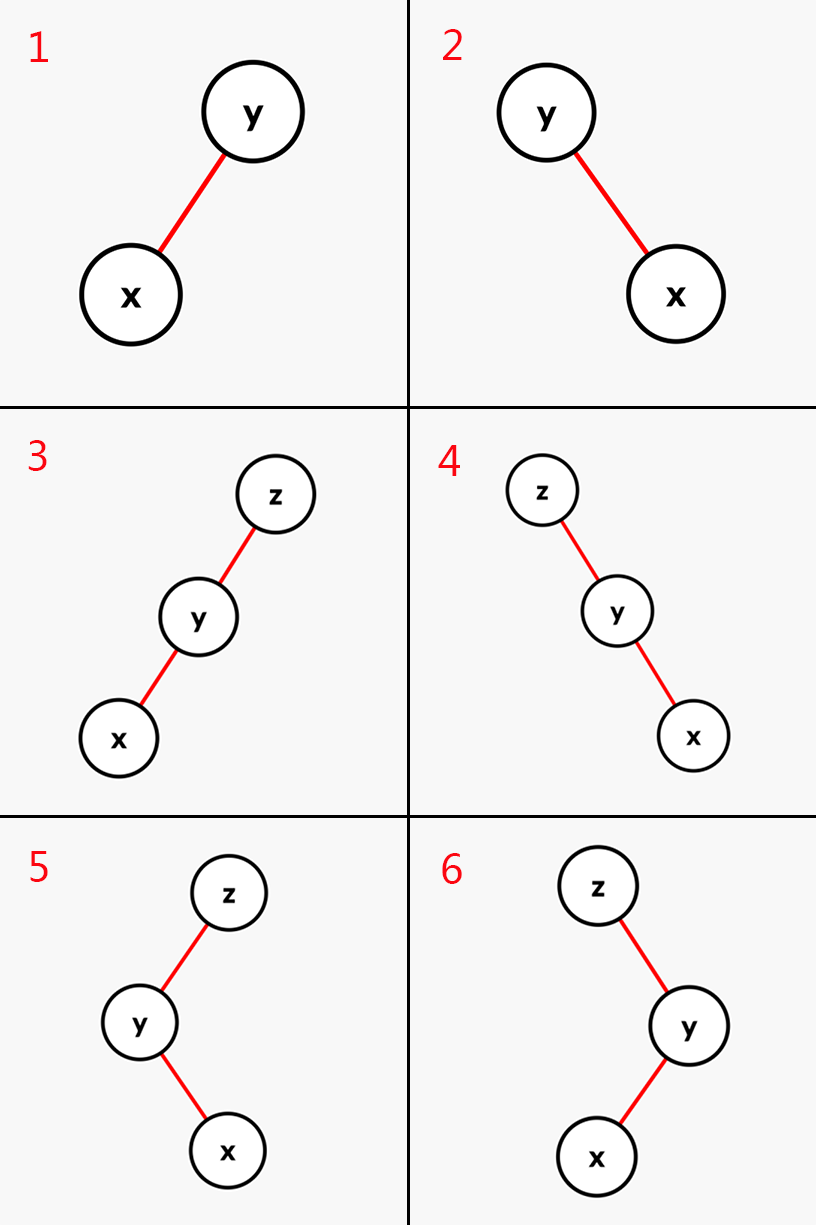
- 一共有6中情况:
Splay伸展
如果 的父亲是根节点,直接将 左旋或右旋(图 1 , 2 )
如果 的父亲不是根节点,且 和父亲的儿子类型相同,首先将其父亲左旋或右旋,然后将 右旋或左旋(图 3 , 4 )
如果 的父亲不是根节点,且 和父亲的儿子类型不同,将 左旋再右旋、或者右旋再左旋(图 5 , 6)
inline void splay(int x) {
for (int f = fa[x]; f = fa[x], f; rotate(x))
if (fa[f]) rotate(lrson(x) == lrson(f) ? f : x);
rt = x;
return;
}