课程表

上午

• 线段树

下午

• 树状数组

晚上

• 考试：线段树$and$树状数组（但是我不用考，哈哈哈哈哈哈）

笔记

1. 线段树

   • 概述：一种二叉树，类似区间树，主要用于解决连续区间的动态查询问题（单点/区间修改、区间最值/求和等等）

   

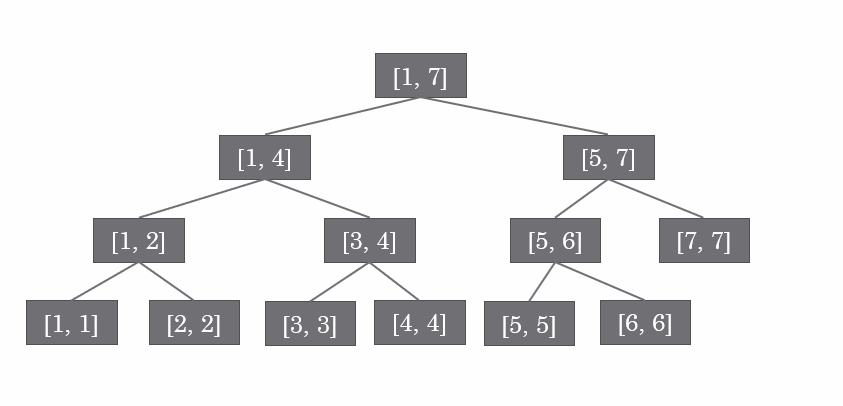
   • 建树：很显然，线段树是个完全二叉树，所以可以直接使用数组在储存这个树，连边都不用存了。
   CPP

   int SegTree[N];

   ​

   ​ 对于这么一个树，结点$[i]$左孩子是$[2*i]$，右孩子是$[2*i+1]$。完整构造函数：

   CPP

   const int  N=1000;
   int Tree[N];
   struct Segment_Tree{
       int sum[N<<2];//一般开2倍即可，开4倍比较保险
       inline void pushup(int o){
           sum[o]=sum[o*2]+sum[o*2+1];
       }
       inline void build (int o,int l,int r){
           if (l==r){
               sum[o]=SegTree[l];
               return;
           }
           int mid=(l+r)>>1;
           build (o*2,l,mid);
           build (o*2+1,mid+1,r);
           pushUp(o);
       }
   };

   • 各种基本操作：

     • 查询线段树（最大/最小）：只有查询，不包括建树！！
     CPP

     #define INF 1<<31
     const int N=1000;
     int Tree[N];
     struct Segment_Tree{
         #define lson (o<<1)
         #define rson (o<<1|1)
         int Min[N<<2];//这里并没有写Min的初始化代码
         inline int queryMin(int o,int l,int r,int ql,int qr){//当前树节点，左右边界，原查询边界
             if (ql<=1&&r<=qr) return Min[o];
             int mid=(l+r)>>1,ans=INF;
             if (ql<=mid) ans=min(ans,queryMin(lson,l,mid,ql,qr));
             if (qr>mid) ans=min(ans,queryMin(rson,mid+1,r,ql,qr));
             //分开查找左右子树
             return ans;
         }
     };

     • 单节点修改：这里演示最小值，单节点增加的情况，要随机应变！
     CPP

     #define INF 1<<31
     const int N=1000;
     int Tree[N];
     struct Segment_Tree{
         #define lson (o<<1)
         #define rson (o<<1|1)
         int Min(N<<2);//同样不包括建树
         inline void pushUp(int o){
             Min[o]=min(Min[lson],Min[rson]);
         }
         inline void change(int o,int l,int r,int q,intv){
             //修改位置q，增加v
             if (l==r){
                 Min[o]+=v;
                 return;
             }
             int mid=(l+r)>>1;
             if (q<=mid) change (lson,l,mid,q,v);
             else change (rson,mid+1,r,q,v);
             pushUp(o);//向上更新
         }
     };

     • 区间修改：【洛谷】3372【模板】线段树1
       • 补充：上面都没有说线段树最重要的最精髓的地方，那就是$lazy$标记。如果某个父节点的子树并不需要立即更新，只需要在父节点上面打一个$lazy$标记，在真正需要查询的时候在把标记传递到子节点。相应的子节点也要看情况判断是否需要继续pushdown，如果不用就打上$lazy$标记。记得pushdown后，父节点的$lazy$要消掉！
     CPP

     #include<cstdio>
     #include<iostream>
     #include<algorithm>
     
     #define lson (o<<1)
     #define rson (o<<1|1)
     
     using namespace std;
     
     
     const int MAX=110000;
     long long sumv[500000], add[500000];
     
     void pushup(int o){
         sumv[o]=sumv[lson]+sumv[rson];
     }
     
     void pushdown(int o,int l,int r){
         int k=(l+r)>>1;
         if(!add[o]) return;
         add[lson]+=add[o];
         add[rson]+=add[o];
         sumv[lson]+=add[o]*(k-l+1);
         sumv[rson]+=add[o]*(r-k);
         add[o]=0;
     }
     
     void build(int o,int l,int r){
         add[o]=0;
         if(l==r){
             scanf("%lld",&sumv[o]);
             return;
         }
         int mid=(l+r)>>1;
         build(lson,l,mid);
         build(rson,mid+1,r);
         pushup(o);
     }
     
     void optadd(int o,int l,int r,int ql,int qr,int v){
         if(ql<=l&&qr>=r){
             add[o]+=v;
             sumv[o]+=v*(r-l+1);
             return;
         }
         int mid=(l+r)>>1;
         pushdown(o,l,r);
         if(ql<=mid) optadd(lson,l,mid,ql,qr,v);
         if(qr>mid)  optadd(rson,mid+1,r,ql,qr,v);
         pushup(o);
     }
     
     long long que(int o,int l,int r,int ql,int qr){
         if(ql<=l&&qr>=r) return sumv[o];
         pushdown(o,l,r);
         int mid=(l+r)>>1;
         long long ans=0;
         pushup(o);
         if(ql<=mid) ans+=que(lson,l,mid,ql,qr);
         if(qr>mid)  ans+=que(rson,mid+1,r,ql,qr);
         return ans;
     }
     
     int main(){
         int n,m;
         scanf("%d%d",&n,&m);
         build(1,1,n);
         for(int i=1;i<=m;i++){
             int L,R,C,Q;
             scanf("%d",&Q);
             if(Q==1){
                 scanf("%d%d%d",&L,&R,&C);
                 optadd(1,1,n,L,R,C);
             }
             else if(Q==2){
                 scanf("%d%d",&L,&R);
                 printf("%lld\n",que(1,1,n,L,R));
             }
         }
         return 0;
     }

2. 树状数组

   • 定义：树状数组是一棵“树”，有点像线段树，但是和完全二叉树的储存还是有很大区别的。

     

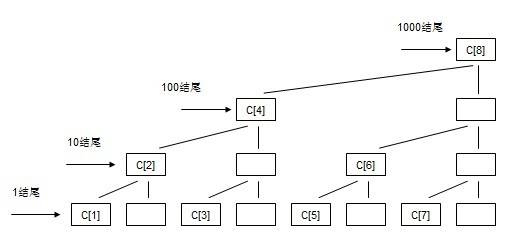
     • 图中空白的格子不储存在数组中！我们把这些数组的下标转化为二进制看看：

       1 => 00000001

       2 => 00000010

       3 => 00000011

       4 => 00000100

       5 => 00000101

       6 => 00000110

       7 => 00000111

       8 => 00001000

       结合上面的图，你会惊奇的发现，c[i]储存$2^{lowbit(i)-1}$个数据的和，储存的范围是$data[i-2^{lowbit(i)-1}+1].....data[i]$。

     • 于是，我们可以定义树状数组中每一个元素$c[x]= \sum\limits_{i=2^{lowbit(x)-1}}^x data[i]$。

   • 单点修改：

   CPP

   inline void Update(int i,int value){//i是修改位置，value是增加数值
       while (i<=n){
           c[i]+=value;
           i+=lowbit(i);
       }
       return;
   }

   • 区间查询：计算$1 \Rightarrow i$的和，若需要$l \Rightarrow r$的区间和，$ans=Sum(r)-Sum(l-1)$。
   CPP

   inline int Sum(int i){
       int sum=0;
       while (i>0){
           sum+=c[i];
           i-=lowbit(i);
       }
       return sum;
   }

总结

• 数据结构挺恶心的，但是不得不说还是挺重要的，这种高级数据结构在省选比较多，光打个数据结构至少都有黄题的难度了。$emm$，有时间多做题吧QAQ