课程表

上午

• 考试$QAQ$

下午

• 考试$QAQ$

晚上

• 讲评考试$QAQ$（其实在听讲座）

考试

上午

1. 刷题计划（problem.cpp/problem.in/problem.out）

   • 时空限制：1000ms/256MB

   • 题面：王队在做题，他想把最新的前20道提交了没有$AC$过的题目列出来。如果没有20道，就只输出全部。输入会有如下几个操作：

     • 1 x：王队提交了题号为$x$的$Accepted$的代码
     • 2 x：王队提交了题号为$x$的$UnAccepted$的代码
     • 3：王队现在想知道最新的前20道没有$AC$的题号

   • 输入格式：第一行为两个整数：$n,m$。接下来的$m$行，每行一个命令。

   • 输出格式：对于每一个3的命令的结果，表示未$AC$的题目。保证每一个3命令时至少有一个未解决的题目。

   • 输入样例：

     10000 12

     2 1

     3

     2 9999

     3

     1 1

     3

     2 1

     3

     2 10000

     3

     2 9999

     3

   • 输出样例：

     1 9999 1 9999 9999 10000 9999 9999 10000

   • 数据范围：对于$30$%的数据，有$n\leq10^5$；对于$100$的数据，有$n\leq10^9$，$m\leq10^2$。

   • 分析：应该随便搞吧，$m$很小，所以把重点放在$m$上就可以了，$n$很大，不能用桶。

   • $Code$：（期望：100分）
   CPP

   #include <iostream>
   #include <cstdio>
   #include <algorithm>
   using namespace std;
   struct node{
       int Time,Name;
       bool AC;
   }Q[10005];
   int n,m,type,Task,cnt,time;
   int Test[10005],Testcnt;
   int AC[10005],ACcnt;
   inline void Clear(){
       for (int i=1;i<=ACcnt;i++)
           for (int j=1;j<=cnt;j++)
               if (AC[i]==Q[j].Name)
                   Q[j].AC=true;
       return;
   }
   bool cmp(node a,node b){
       return a.Time>b.Time;
   }
   int main(){
       freopen("problem.in","r",stdin);
       freopen("problem.out","w",stdout);
       scanf("%d%d",&n,&m);
       for (int i=1;i<=m;i++){
           scanf("%d",&type);
           if (type==1){
               scanf("%d",&AC[++ACcnt]);
               continue;
           }
           if (type==2){
               scanf("%d",&Task);
               cnt++;
               Q[cnt].Name=Task;
               Q[cnt].Time=++time;
               Q[cnt].AC=false;
               continue;
           }
           if (type==3){
               int ans=0;
               sort (Q+1,Q+cnt+1,cmp);
               Clear();
               Testcnt=0;
               for (int j=1;j<=cnt;j++){
                   if (!Q[j].AC){
                       bool flag=false;
                       for (int k=1;k<=Testcnt;k++)
                           if (Test[k]==Q[j].Name){
                               flag=true;
                               break;
                           }
                       if (flag) continue;
                       printf ("%d ",Q[j].Name);
                       Test[++Testcnt]=Q[j].Name;
                       ans++;
                       if (ans>=20) break;
                   }
               }
               printf("\n");
           }
       }
       fclose(stdin);
       fclose(stdout);
       return 0;
   }

2. 最优交换（swap.cpp/swap.in/swap.out）

   • 时空限制：1000ms/256MB

   • 题面：王队有一个长度为$n$的正整数。他会对这个正整数进行一系列操作，一次操作可以交换该正整数的两个相邻的数位。然而时间有限，他只被允许进行不超过$k$次这样的操作。王队想知道，操作后得到的数最大是多少。

   • 输入格式：第一行一个整数$T$，表示数据组数。每组数据包含一行2个整数，第一个是王队的正整数，第二个是$k$。

   • 输出格式：对于每组数据，输出一行一个正整数，表示得到的最大数是多少。

   • 输入样例：

     2

     1432 2

     4321 2

   • 输出样例：

     4312

     4321

   • 数据说明：对于20%的数据，有$n\leq10,k\leq3$。对于另外20%的数据，T=1且数据随机生成。对于另外20%的数据，$k\leq30$。对于另外20%的数据，$n\leq18$。对于全部数据，$T\leq1000,n\leq 50,0 \leq k \leq 10^5$。

   • 分析：正解应该是贪心，但是我不知道怎么贪$QAQ$，考试的时候甚至还想到了$dp$？！当然我不会打$dp$，我只打了一个暴力。

   • $Code$：（期望：20分）
   CPP

   #include <iostream>
   #include <cstdio>
   #include <cstring>
   using namespace std;
   int T,k,len;
   string str,Maxstr;
   string Max(string a,string b){
       if (a>b) return a;
       return b;
   }
   void dfs(string str,int deep){
       if (deep>k){
           Maxstr=Max(Maxstr,str);
           return;
       }
       for (int i=0;i<len-1;i++){
           swap(str[i],str[i+1]);
           dfs(str,deep+1);
           swap(str[i],str[i+1]);
       }
       return; 
   }
   int main(){
       freopen("swap.in","r",stdin);
       freopen("swap.out","w",stdout);
       scanf("%d",&T);
       while (T--){
           cin >>str;
           scanf("%d",&k);
           len=str.length();
           dfs(str,1);
           
           
           cout <<Maxstr<<endl;
       }
       fclose(stdin);
       fclose(stdout);
       return 0;
   }

3. 矩阵（matrix.cpp/matrix.in/matrix.out）

• 时空限制：2000ms/256MB

• 题面：有$n \times m$的矩阵，你从左上角走到右下角，每次只能向下或向右走。每个点有一个重量为$v_{i,j}$的价值为$w_{i,j}$的一个物品，你有一个容量为$S$的背包，经过一个点你可以将此点的物品放入背包，求背包物品的最大价值和。

• 输入格式：第一行三个数$n,m,S$。下面$n$行，每行$m$个数，第$i+1$行第$j$个数表示$v_{i,j}$。下面$n$行，每行$m$个数，第$i+n+1$行第$j$个数表示$w_{i,j}$。

• 输出格式：一个数表示最大值。

• 输入样例：

  3 4 5

  1 2 1 1

  2 3 1 2

  3 2 2 2

  2 3 4 2

  1 4 5 1

  10 1 2 1

• 输出样例：

  14

• 数据范围：30%：$n \times m \leq 50 ,S \leq 100$；60%：$n,m \leq 100,S\leq 200$；100%：$n,m \leq 400,0 \leq v_{i,j},w_{i,j}\leq 1000,S\leq 400$。

• 分析：这是一道裸的背包问题，原来内存限制是128MB，后来变成256MB了，所以3维的$400 \times 400 \times 400$的$dp$数组是可以开的，时间也从1s到了2s。所以考试里调出来的$dp$应该没有什么问题$QAQ$。

• $Code$：（期望：100分）

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
int n,m,S,ans;
struct node{
    int v,w;
}G[405][405];
int dp[405][405][405];
int main(){
    freopen("matrix.in","r",stdin);
    freopen("matrix.out","w",stdout);
    scanf("%d%d%d",&n,&m,&S);
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
            scanf("%d",&G[i][j].v);
    for (int i=1;i<=n;i++)
        for (int j=1;j<=m;j++)
            scanf("%d",&G[i][j].w);
    for (int s=0;s<=S;s++){
        for (int i=1;i<=n;i++){
            for (int j=1;j<=m;j++){
                if (G[i][j].v<=s)
                    dp[i][j][s]=max(max(dp[i-1][j][s-G[i][j].v],dp[i][j-1][s-G[i][j].v])+G[i][j].w,max(dp[i][j-1][s],dp[i-1][j][s]));
                else dp[i][j][s]=max(dp[i][j-1][s],dp[i-1][j][s]);
            }
        }
    }
    
    printf ("%d\n",dp[n][m][S]);
    fclose(stdin);
    fclose(stdout);
    return 0;
}

4. 格点统计（count.cpp/count.in/count.out）

   • 时空限制：1000ms/256MB

   • 题面：求第一象限中，位于反比例函数$xy=k$的下方（含边界）的格点的个数。

   • 输入格式：一个正整数$k$。

   • 输出格式：一个整数，要模998244353。

   • 输入样例：

     1. 3

     2. 4

   • 输出样例：

     1. 5

     2. 8

   • 数据范围：

     

   • 分析：数论找规律吧....反正我推出这么一个东西：

     CPP

     for (unsigned long long i=1;i<=Sqrt;i++){
         ans+=k-2*i+1;
         if (ans>Mod) ans=ans%Mod;
     }
     ans++;
     ans*=2;
     ans-=Psum;//x=y的个数
     ans=ans%Mod;

     不过测出来证明是错的$QAQ$

5. 产品排序（product.cpp/product.in/product.out）

   • 时空限制：1000ms/256MB

   • 题面：你是一个公司的员工，你会按时间顺序受到一些产品的订单，你需要用一个栈来改变这些订单的顺序（每个产品都必须入栈和出栈一次）。按初始顺序，每次可以将一个产品入栈，或将栈顶产品弹至现在的序列末尾。每个产品有一个制作时间$t_i$和单位时间惩罚值$d_i$，总的惩罚值为$\sum^{n}_{i=1}(s_i \times d_i)$，其中$s_i$为第$i$个产品的完成时间，你需要最小化总的惩罚值。

   • 输入格式：第一行一个数$n$，表示产品个数。接下来$n$行，每行两个数表示$t_i,d_i$。

   • 输出格式：一行一个数表示最小的总惩罚值。

   • 输入样例：

     4

     1 4

     3 2

     5 2

     2 1

   • 输出样例：

     40

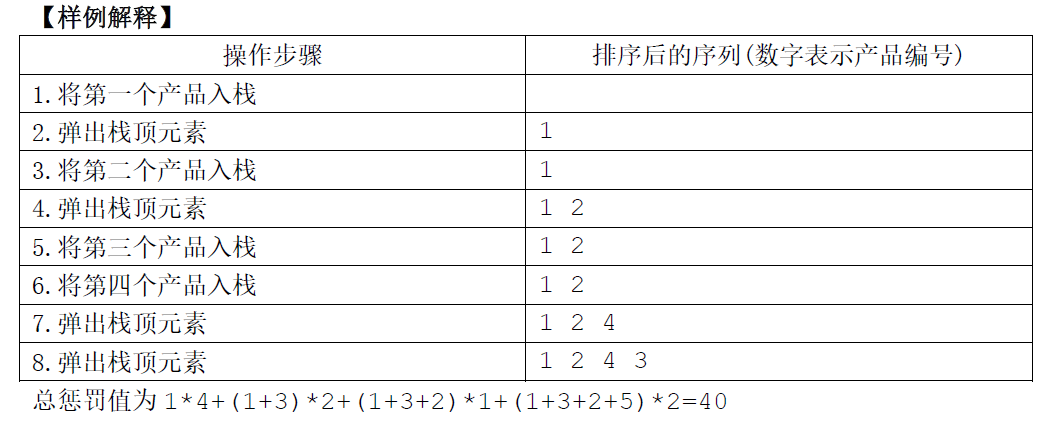
   • 样例解释：

     

   • 数据范围：30%：$n \leq 15$；50%：$n \leq 100$；100%：$n \leq 200,t_i,d_i \leq 1000$。

   • 分析：题目是看懂了，但是没有任何思路。。。。最后时间不够连暴力都没打$QAQ$

6. 电话线铺设（telephone.cpp/telephone.in/telephone.out）

   • 时空限制：2000ms/256MB

   • 题面：一个新的小区建成，该小区有$n$栋房子。由于是新小区，还没有铺设电话线，所以社区负责人联系到了工头王队，希望王队以最小的代价铺设电话线。王队的工作就是用$