2019.8.1 集训解题报告

2019 年 8 月 1 日 星期四
/ , , , , , , , ,

2019.8.1 集训解题报告

Luogu P1801 黑匣子

这道题是分在试炼场的”堆“模块里面，太菜了，没有想出来。

看了题解后也感觉自己想到边了，既然是求第 kk 小，那么对于堆这么一个堆顶是 最大/最小 的一个结构来说，应该要用一个堆直接储存目前的前 kk 小，那么，在输出的时候，只需要输出堆顶就可以了。所以，这样就可以很自然的想到要用两个堆，一个堆 AA，用作前面的用途，另一个堆 BB要储存当前，前 kk 小以外的其他数据。每次 GetGet 一次后，就要把 AA 的大小扩大 1 个，保证堆顶永远是第 kk 小。

然后我们就可以得到一个似乎叫对顶堆的东西，如图：

对顶堆
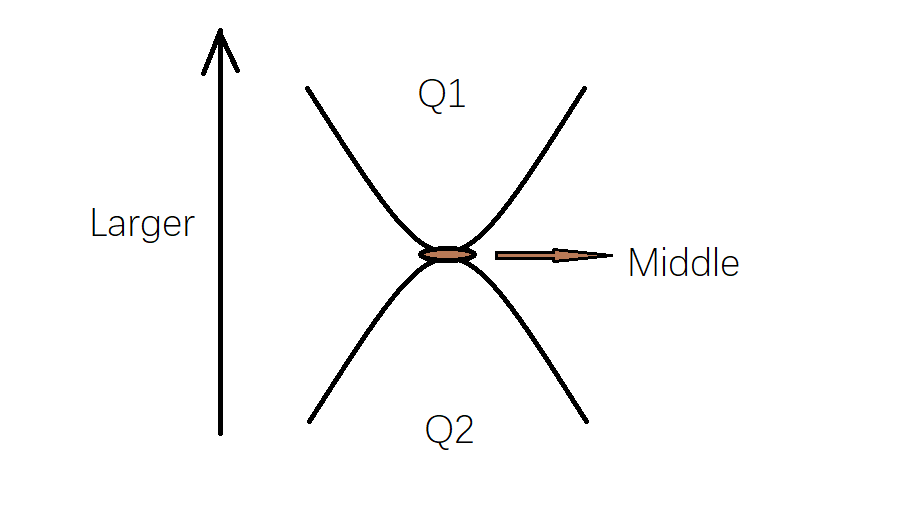
对顶堆

把这两个堆这样放，就更好理解了，我们每次 pushpush 时，只需要维护中间两个堆顶，使这一整个对顶堆保持类似堆得性质（从下往上依次 变大/变小）。

维护两个堆顶非常简单，只需要判断两个堆顶的大小是否合法即可，不合法就交换，一直到合法。

Code：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
const int MAXN=2e5+5;
int m,n,a[MAXN],u[MAXN],cnt_a,cnt_u=1;
int main(){
    priority_queue<int>A;
    priority_queue<int , vector <int> , greater <int> >B;
    scanf ("%d%d",&m,&n);
    for (int i=1;i<=m;i++)
        scanf ("%d",&a[i]);
    for (int i=1;i<=n;i++)
        scanf ("%d",&u[i]);
    for (cnt_a=1;cnt_a<=m;cnt_a++){
        while (cnt_a-1==u[cnt_u]){
            cnt_u++;
            int t=B.top();
            B.pop();
            A.push(t);
            printf ("%d\n",A.top());
        }
        B.push(a[cnt_a]);
        if (A.empty()) continue; 
        while (A.top()>B.top()){
            int t=B.top();
            B.pop();
            B.push(A.top());
            A.pop();
            A.push(t);
        }
    }
    while (cnt_a-1==u[cnt_u]){
        cnt_u++;
        int t=B.top();
        B.pop();
        A.push(t);
        printf ("%d\n",A.top());
    }
    return 0;
}
  • 代码写的非常丑，当然这道题可以使用平衡树，用 TreapTreap 就绰绰有余了。

考试

  • 有三道题，如果我题目没有看错的话，应该不是特别毒瘤（等我看完考试成绩后再说），

水叮当的舞步

水叮当的舞步
水叮当的舞步

题目里面已经提到联通块了，所以用 dfsdfs 或者 bfsbfs 求出每种颜色联通块的个数。看到分数后，又去看了下 datadata ，然后我发现看题看错了 qwqqwq

Update（2019.8.14）

看完题解之后：A 组我 cnm！

要用 迭代加深启发式搜索 。。。。。

nmsl。。。

就记一下纪中的题解：等我学完了什么 IDA∗IDA* 、估价函数再回来写这道题......

Solution From lydrainbowcatlydrainbowcat 类型：IDA* (迭代加深启发式搜索)

  1. 枚举每次选取了哪种颜色，然后找出左上角的格子所在的联通块，改变颜色。 为了避免来回改变、搜索深度过大，采用迭代加深的 dfsdfs 限制搜索步数。 迭代加深也就是，依次限制搜索深度为 0、1、2、3…… 进行搜索，搜索过程中发现深度超过限制就马上退出。只要搜索成功就找到了答案，也可以立即退出。
    • 期望得分：0~10分。
  2. 加入一个小剪枝：如果改变颜色后，左上角格子所在的联通块大小没有改变，可以剪枝。这样可以避免来回往复地搜索。
    • 期望得分：10~20分。
  3. 采用 IDA∗IDA* 算法，设计估价函数。可以发现如果当前矩阵中除了左上角的联通块之外，共有 MM 种颜色，那么还需要的步数不小于 MM。因此如果当前搜索深度 ++ 估价函数的值 >> 深度限制，可以回溯。
    • 期望得分：50~70分。
  4. 我们可以发现，每次寻找左上角的格子所在的联通块耗费的时间常数巨大。因此我们在这里寻求突破。 我们引入一个 N×NN \times N的 vv 数组。左上角的格子所在的联通块里的格子标记为 1。左上角联通块周围一圈格子标记为 2，其它格子标记为 0。如果某次选择了颜色 cc ，我们只需要找出标记为 2 并且颜色为 cc 的格子，向四周扩展，并相应地修改 vv 标记，就可以不断扩大标记为 1 的区域，最终如果所有格子标记都是 1，那么显然找到了答案。
    • 期望得分：90~100分。

Vani 和 Cl2 捉迷藏

写了一个 20 分的，然后就超时了。

先用 FloydFloyd 跑一遍题目中的 DAGDAG，然后就可以得到一个被补完的邻接矩阵。这个时候，就可以知道任意两点之间的联通关系。最简单粗暴的方法就是我考场上写个 dfsdfs ，依次判断是否完全互不相连就可以了，但是只有 20 分。

因此，我们就可以把这样的图看做二分图来匹配，最大匹配就是最多能选出多少个点相连。似乎最简单的就是匈牙利算法，以前学过，但是我忘了 qwq。需要一个公式： DAG的最小路径覆盖数=DAG图中的节点数-相应二分图中的最大匹配数 这里是 DAGDAG 普通的有向图不是这样的，然后就可以了。

后面因为不服我的代码，后面发现，因为考试时有个队列因为怕爆，加了一个次方，后面减去之后，分数直接到 60 。看来以后没有用的东西就不要去做了 qwqqwq 。

Test′sTest's CodeCode：60%
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
const int MAXN = 2e2+5;
const int MAXM = 3e4+5;
const int MAXQ = 2e6+5;
struct Edge{
    int v,next;
}edge[MAXM];
bool flag[MAXN][MAXN],bz[MAXN];
int cnt,ans,head[MAXN],m,n,Max;
int que[MAXN],tail;
inline void AddEdge(int u, int v){
    cnt++;
    edge[cnt].v=v;
    edge[cnt].next=head[u];
    head[u]=cnt;
    return;
}
void dfs1(int u){
    for (int i=head[u];i!=0;i=edge[i].next){
        int v=edge[i].v;
        for (int j=1;j<=tail;j++){
            int t=que[j];
            flag[t][v]=true;
        }
        que[++tail]=v;
        dfs1 (v);
        tail--;
    }
    return;
}
void dfs2 (int u){
    for (int i=1;i<=n;i++){
        if (i==u) continue;
        if (bz[i]) continue;
        bool check=false;
        for (int j=1;j<=tail;j++){
            int t=que[j];
            if (flag[i][t]||flag[t][i]){
                check=true;
                break;
            }
        }
        if (check) continue;
        ans++;
        Max=max(Max,ans);
        bz[i]=true;
        que[++tail]=i;
        dfs2(i);
        tail--;
        ans--;
        bz[i]=false;
    }
    return;
}
int main(){
    scanf ("%d%d",&n,&m);
    for (int i=1;i<=m;i++){
        int u,v;
        scanf ("%d%d",&u,&v);
        AddEdge(u,v);
    }
    for (int i=1;i<=n;i++){
        memset(que,0,sizeof (que));
        tail=0;
        que[++tail]=i;
        dfs1(i);
    }
    for (int i=1;i<=n/2+1;i++){
        memset(que,0,sizeof (que));
        ans=1;
        tail=0;
        bz[i]=true;
        que[++tail]=i;
        dfs2 (i);
        bz[i]=false;
    }
    printf ("%d\n",Max);
    return 0;
}
FixedFixed CodeCode：100%
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
const int MAXN = 2e2+5;
bool flag[MAXN][MAXN],bz[MAXN];
int ans,m,n;
int link[MAXN];
int find (int x) {
    for (int i=1;i<=n;i++) {
        if (!flag[i][x]) continue;
        if (bz[i]) continue;
        bz[i]=true;
        if (!link[i]||find(link[i])){
            link[i]=x;
            return 1;
        }
    }
    return 0;
}
int main(){
    scanf ("%d%d",&n,&m);
    for (int i=1;i<=m;i++){
        int u,v;
        scanf ("%d%d",&u,&v);
        flag[u][v]=true;
    }
    for (int i=1;i<=n;i++)
        for (int j=1;j<=n;j++)
            for (int k=1;k<=n;k++)
                if (flag[i][k]&&flag[k][j]&&i!=j)
                    flag[i][j]=true;
    for (int i=1;i<=n;i++){
        memset(bz,0,sizeof (bz));
        ans +=find (i);
    }
    printf ("%d\n",n-ans);
    return 0;
}
  • 我写的果然又臭又长

三、粉刷匠（集体照）

写了个暴力，没想到暴力的 40 分成了 3 道题目中分最高的 qwqqwq

一看数据就知道是 dpdp 或者数学，当然不可能是数学啦~

所以用 dpdp ，设状态：f[i][j]f[i][j] 为用完 ii 个颜料后，有 jj 个不合法情况的状态。

那么当我们要使用下一个颜料 ii 的时候，把 a[i]a[i] 份颜料分为 kk 组，把 tt 组放在原来不合法的 jj 个空上（这样就可以把它们隔开，就合法了）。

至此，就可以列出一个方程： f[i][j - t + a[i] - k]=f[i-1][j] \times C{a[i]-1}^{k-1} \times C_j^t \times C{s[i]+1-j}^{k-t} Ca[i]−1k−1C_{a[i]-1}^{k-1}：在 a[i]a[i] 中选出 kk 组的情况个数，使用隔板法，小奥知识即可。

CjtC_j^t：在 jj 个不合法的空中选出 tt 个的情况个数。 Cs[i]+1−jk−tC_{s[i]+1-j}^{k-t}：在剩下的空中把没有用完的补上的情况个数。
Update（2019.8.12）

打完代码后顺便记一下求组合的方法：

inline void Init_C () {
    c[0][0] = 1;
    for (long long i = 1; i <= 100; i++) {
        c[i][0] = 1;
        for (long long j = 1; j <= i; j++) {
            c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % Mod;
        }
    }
    return;
}

还有这道题要开 long long qwq

FixedFixed CodeCode：100%
#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;
const long long Mod = 1e9 + 7;
const long long MAXN = 20;
const long long MAXM = 105;

long long n, a[MAXN], s[MAXN], c[MAXM][MAXM];
long long f[MAXN][MAXM];

inline void Init() {
    memset(s, 0, sizeof (s));
    memset(f, 0, sizeof (f));
    return;
}

inline void Init_C () {
    c[0][0] = 1;
    for (long long i = 1; i <= 100; i++) {
        c[i][0] = 1;
        for (long long j = 1; j <= i; j++) {
            c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % Mod;
        }
    }
    return;
}

int main(){
    Init_C ();
    
    long long T;
    scanf ("%lld", &T);
    while (T--) {
        Init ();
        
        scanf ("%lld", &n);
        for (long long i = 1; i <= n; i++) {
            scanf ("%lld", &a[i]);
        }
        
        for (long long i = 1; i <= n; i++) {
            s[i] = s[i - 1] + a[i];
        }
        
        f[0][0] = 1;
        for (long long i = 1; i <= n; i++) {
            for (long long j = 0; j <= s[i - 1]; j++) {
                for (long long k = 1; k <= a[i]; k++) {
                    for (long long t = 0; t <= min (k, j); t++) {
                        f[i][j - t + a[i] - k] += ((f[i - 1][j] * c[a[i] - 1][k - 1] % Mod) * (c[j][t] * c[s[i - 1] + 1 - j][k - t] % Mod)) % Mod;
                        f[i][j - t + a[i] - k] %= Mod;
                    }
                }
            }
        }
        
        printf ("%lld\n", f[n][0]);
    }
    return 0;
}

总结

这么多天以后，我竟然在 8 月 12 日，把第 3 题做出来了 qwq

A 组的人都是神仙，打死我也不去 A 组 > _ <

使用社交账号登录

  • Loading...
  • Loading...
  • Loading...
  • Loading...
  • Loading...