2019.8.10 集训解题报告

2019 年 8 月 10 日 星期六
/ , , , , ,
1

2019.8.10 集训解题报告

菜让我绝望.....

还没有考完试就开始写今天的解题报告，因为剩下两道题我都不会 qwq

考试

洪水

直接 BFSBFS 大暴搜，我考试时唯一的优化就是预处理一下每个格子洪水到达的时间。好像每个人都会这么做吧 qwq，不知道会有多少分......

考完之后我 tm 发现 BFSBFS 的时候没有打标记，直接爆空间。洪水的预处理时有一个显而易见的剪枝，即如果发现当前格子已被更新过，且当前洪水无法进行更优的更新时可以直接返回，我 tm 傻逼的忘记打了。

nmsl，100% ⇒\Rightarrow 0%

Test′sTest's CodeCode：0%
#include <iostream>
#include <cstdio>
#include <queue>

using namespace std;
const int MAXR = 50 + 5;
const int MAXC = 50 + 5;
const int INF = 2e9 + 5;
const int cmp[4][2] = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};

struct Node {
    int x, y;
};
queue<Node> Q;

int r, c, ans, sx, sy, fx, fy, water[MAXR * MAXC][2], cnt_water, cnt;
int flo_time[MAXR][MAXC];

bool flag[MAXR][MAXC];

char g[MAXR][MAXC];

inline bool check_water (int x, int y) {
    if (x < 1 || y < 1 || x > r || y > c) {
        return false;
    }
    if (flag[x][y] || g[x][y] == 'D') {
        return false;
    }
    return true;
}

inline bool check_person (int x, int y) {
    if (x < 1 || y < 1 || x > r || y > c) {
        return false;
    }
    if (flag[x][y] || flo_time[x][y] <= cnt + 1) {
        return false;
    }
    return true;
}

void dfs (int x, int y, int time) {
    for (int i = 0; i < 4; i++) {
        int nx = x + cmp[i][0];
        int ny = y + cmp[i][1];
        if (!check_water(nx, ny)) continue;
        flo_time[nx][ny] = min (flo_time[nx][ny], time + 1);
        flag[nx][ny] = true;
        dfs (nx, ny, time + 1);
        flag[nx][ny] = false;
    }
    return;
}

int main() {
    scanf ("%d%d", &r, &c);
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= c; j++) {
            char ch;
            cin >> ch;
            g[i][j] = ch;
            if (ch == 'S') {
                sx = i;
                sy = j;
            }
            if (ch == 'D') {
                fx = i;
                fy = j;
            }
            if (ch == '*') {
                cnt_water++;
                water[cnt_water][0] = i;
                water[cnt_water][1] = j;
            }
            if (ch == 'X') {
                flag [i][j] = true;
            }
        }
    }
    
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= c; j++) {
            flo_time[i][j] = INF;
        }
    }
    
    for (int i = 1; i <= cnt_water; i++) {
        int x = water[i][0];
        int y = water[i][1];
        flag[x][y] = true;
        flo_time[x][y] = 0;
        dfs (x, y, 0);
    }
    
    Node temp;
    temp.x = sx;
    temp.y = sy;
    flag[sx][sy] = true;
    Q.push(temp);
    
    while (true) {
        if (Q.empty()) {
            printf ("KAKTUS\n");
            return 0;
        }
        int len = Q.size();
        
        while (len--) {
            Node temp;
            temp = Q.front();
            Q.pop();
            
            for (int i = 0; i < 4; i++) {
                Node next;
                next.x = temp.x + cmp[i][0];
                next.y = temp.y + cmp[i][1];
                
                if (!check_person(next.x, next.y)) {
                    continue;
                }
                
                if (next.x == fx && next.y == fy) {
                    printf ("%d\n", cnt + 1);
                    return 0;
                }
                
                Q.push(next);
            }
        }
        
        cnt++;
    }
    return 0;
}
FixedFixed CodeCode：100%
#include <iostream>
#include <cstdio>
#include <queue>

using namespace std;
const int MAXR = 50 + 5;
const int MAXC = 50 + 5;
const int INF = 2e9 + 5;
const int cmp[4][2] = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};

struct Node {
    int x, y;
};
queue<Node> Q;

int r, c, ans, sx, sy, fx, fy, water[MAXR * MAXC][2], cnt_water, cnt;
int flo_time[MAXR][MAXC];

bool flag[MAXR][MAXC];

char g[MAXR][MAXC];

inline bool check_water (int x, int y) {
    if (x < 1 || y < 1 || x > r || y > c) {
        return false;
    }
    if (flag[x][y] || g[x][y] == 'D') {
        return false;
    }
    return true;
}

inline bool check_person (int x, int y) {
    if (x < 1 || y < 1 || x > r || y > c) {
        return false;
    }
    if (flag[x][y] || flo_time[x][y] <= cnt + 1) {
        return false;
    }
    return true;
}

void dfs (int x, int y, int time) {
    for (int i = 0; i < 4; i++) {
        int nx = x + cmp[i][0];
        int ny = y + cmp[i][1];
        if (!check_water(nx, ny)) continue;
        if (flo_time[nx][ny] > time + 1) {
            flo_time[nx][ny] = time + 1;
        }
        else if (flo_time[nx][ny] != INF && flo_time[nx][ny] <= time + 1) {
            return;
        }
        flag[nx][ny] = true;
        dfs (nx, ny, time + 1);
        flag[nx][ny] = false;
    }
    return;
}

int main() {
    scanf ("%d%d", &r, &c);
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= c; j++) {
            char ch;
            cin >> ch;
            g[i][j] = ch;
            if (ch == 'S') {
                sx = i;
                sy = j;
            }
            if (ch == 'D') {
                fx = i;
                fy = j;
            }
            if (ch == '*') {
                cnt_water++;
                water[cnt_water][0] = i;
                water[cnt_water][1] = j;
            }
            if (ch == 'X') {
                flag [i][j] = true;
            }
        }
    }
    
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= c; j++) {
            flo_time[i][j] = INF;
        }
    }
    
    for (int i = 1; i <= cnt_water; i++) {
        int x = water[i][0];
        int y = water[i][1];
        flag[x][y] = true;
        flo_time[x][y] = 0;
        dfs (x, y, 0);
    }
    
    Node temp;
    temp.x = sx;
    temp.y = sy;
    flag[sx][sy] = true;
    Q.push(temp);
    
    while (true) {
        if (Q.empty()) {
            printf ("KAKTUS\n");
            return 0;
        }
        int len = Q.size();
        
        while (len--) {
            Node temp;
            temp = Q.front();
            Q.pop();
            
            for (int i = 0; i < 4; i++) {
                Node next;
                next.x = temp.x + cmp[i][0];
                next.y = temp.y + cmp[i][1];
                
                if (!check_person(next.x, next.y)) {
                    continue;
                }
                
                if (next.x == fx && next.y == fy) {
                    printf ("%d\n", cnt + 1);
                    return 0;
                }
                
                flag[next.x][next.y] = true;
                Q.push(next);
            }
        }
        
        cnt++;
    }
    return 0;
}

邦德

应该是 dpdp ，但是我不会设计这个状态啊 qwq，跳过跳过.....

话说这题大暴搜可以 95 ？！早知道我也去暴搜 qwq

这道题就是装压 dpdp ，这道题可以看做是 八皇后 的改版，可以把数据看做一个棋盘，然后把每一行是否占用转成 0/1 状态压缩一下。

设计状态：f[k]f[k] 表示 kk 状态的最大概率，kk 表示所有任务的选择情况，如果已被选择，就是 1 ，否则是 0 。

这样就可以列出一个方程： f[k] = max { f[k], f[k - (1 << (i))] \times a[x][i] } xx 表示当前人物，ii 表示当前枚举的任务，看看是否最优。

FixedFixed CodeCode：100%
#include <iostream>
#include <cstdio>

using namespace std;
const int MAXN = 25;
const int MAXB = 1024 * 1024 + 5;

int n;

double f[MAXB], a[MAXN][MAXN];

double fmax (double a, double b) {
    return (a > b ? a : b);
}

int main() {
    scanf ("%d", &n);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            scanf ("%lf", &a[i][j]);
            a[i][j] /= 100.0;
        }
    }
    
    f[0] = 100.0;
    for (int k = 1; k < (1 << n); k++) {
        int x = 0;
        for (int i = 1; i <= n; i++) {
            if (k & (1 << (i - 1))) {
                x++;
            }
        }
        
        for (int i = 1; i <= n; i++) {
            if (k & (1 << (i - 1))) {
                f[k] = fmax (f[k], f[k - (1 << (i - 1))] * a[x][i]);
            }
        }
    }
    
    printf ("%.6lf\n", f[(1 << n) - 1]);
    return 0;
}

餐桌

直接一直找矩形，应该没有问题吧，但是好像数据有点大，会超时？？？

这题要用 单调栈 ，我为什么没有听过这个东西？？（雾）

去 OI Wiki 补了一下单调栈，说起来也挺简单的，就是一定要满足栈中的东西满足单调性，和单调队列差不多。单调栈如果要 push 进去一个放在 top 不满足单调性的数据，就需要把下面的不满足的 pop 上来，知道 push 进去之后满足单调性。

然后这道题就和 POJ 2559 非常相似了，POJ 上是求面积，但是这里是求周长。POJ 是每次把 pop 的时候把答案更新一下，然后把长度加给后一个 top 对应的值，这里有一篇 详情 讲 POJ 2559 的。

但是，对于这道题来说有一点问题，就是每一个宽度为 1 的长方形都是我们自己从原图中切出来的，有一些本来是相连的，切割以后放在一起时，就可能把原来不相连的放在一起，相连的又分开了。然后现在我还没有想到好的解决方法 qwq

（2019.8.11）看完一些公开的代码后，知道怎么搞了，可以在没有相邻的地方中间可以插入一些高度为 0 的长方形，这样就不会连在一起，然后切取长方形的时候，注意按顺序切就可以了。

这题还有一个做法，有点类似我在考试上用的模拟，叫做 悬线法 dpdp 。这是纪中 dalaodalao LZCLZC 提出的，我没有听过，不过按照 dalaodalao 的解释：

就是说，对于每一个点，求出其向上扩展的最高高度，然后求出这个高度向左向右最多可以扩展到哪里。

设 hi,jh_{i,j} 表示 (i,j)(i,j) 向上能扩展的最高高度， li,j,ri,jl_{i,j},r_{i,j} 分别表示 (i,j)(i,j) 在向上扩展了 hi,jh_{i,j} 的前提下向左向右最多可以扩展到的位置。

然后这三个值都随便 DP 啊，于是最后 xjb 合并一下答案就没了。

—— LZC

所以说，复杂度就是 O(n3)O(n^3) 咯~~，不过我感觉单调栈更 nbnb 一点。明天有时间把悬线法也打了 qwq

Test′sTest's CodeCode：15%
#include <iostream>
#include <cstdio>

using namespace std;
const int MAXN = 1e3 + 5;

int r, c, ans;

bool g[MAXN][MAXN];

int main() {
    scanf ("%d%d", &r, &c);
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= c; j++) {
            char ch;
            cin >>ch;
            if (ch == '.') {
                g[i][j] = true;
            }
        }
    }
    
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= c; j++) {
            if (!g[i][j]) continue;
            
            int y = j + 1;
            while (g[i][y]) {
                y++;
            }
            y--;
            int x = i;
            while (g[x][j]) {
                x--;
            }
            x++;
            
            int k;
            for (k = x; g[k][j]; k++) {
                bool flag = true;
                for (int l = j; l <= y; l++) {
                    if (!g[k][l]) {
                        flag =false;
                        break;
                    }
                }
                if (!flag) {
                    ans = max (ans, 2 * (x - (k - 1) + 1) + 2 * (y - j + 1));
                    break;
                }
            }
            
            if (k > r) {
                ans = max (ans, 2 * (r - i + 1) + 2 * (y - j + 1));
            }
            if (!g[k][j]) {
                ans = max (ans, 2 * (k - 1 - i + 1) + 2 * (y - j + 1));
            }
        }
    }
    
    printf ("%d\n", ans - 1);
    return 0;
}
FixedFixed CodeCode：100% （单调栈）
#include <iostream>
#include <cstdio>

using namespace std;
const int MAXN = 2e3 + 5;

struct Node {
    int x, y;
};
Node stack[MAXN], temp[MAXN];

int r, c, ans, cnt, top;

bool g[MAXN][MAXN];

int main() {
    scanf ("%d%d", &r, &c);
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= c; j++) {
            char ch;
            cin >>ch;
            if (ch == '.') {
                g[i][j] = true;
            }
        }
    }
    
    for (int i = 1; i <= r; i++) {
        cnt = 0;
        for (int j = 1; j <= c; j++) {
            temp[j].x = 1;
            if (g[i][j]) {
                temp[j].y++;
            }
            else {
                temp[j].y = 0;
            }
        }
        
        for (int j = 1; j <= c; j++) {
            int sum = 0;
            while (stack[top].y > temp[j].y) {
                sum += stack[top].x;
                ans = max (ans, (stack[top].y + sum) * 2);
                top--;
            }
            
            top++;
            stack[top].x = sum + temp[j].x;
            stack[top].y = temp[j].y;
        }
        
        int sum = 0;
        while (stack[top].y > 0) {
            sum += stack[top].x;
            ans = max (ans, (stack[top].y + sum) * 2);
            top--;
        }
        top = 0;
    }
    
    printf ("%d\n", ans - 1);
    return 0;
}

自行车比赛

感觉和昨天的 T2 有点像，如果是一类题型的话，做法应该也是什么 Floyd+Floyd+ 矩阵快速幂。这道题都不用拆边了，但是还要判断一下重边、环的情况。昨天没有订 T2 ，所以不知道这题考试时直接输出 inf 能水几分 QAQ

这题从某种意义上来说非常的水，因为数据中根本没有 inf 的情况，所以说这就转化成了直接在 DAGDAG 中求路径个数了，直接拓扑排序一下，知道枚举顺序，然后直接递归到终点即可。

但是如果真的有 inf 的数据的话，就需要用 tarjantarjan 了。为什么说直接搜索或者拓扑判环不可以呢？因为可能环不在起点到终点的路径上。

如图：

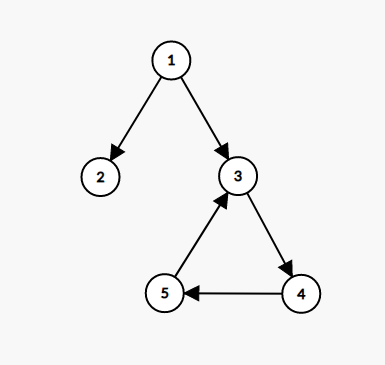
那个环是不需要过去的，所以不会 inf 。于是就只能 tarjantarjan 了 QAQ

等等......我晚上翻到论坛时.....

但是不用 tarjantarjan 怎么搞啊 qwq，可以 xjb 乱搞那这题也太水了吧.......我太菜了 QAQ

先抛开环这个问题，我先打了个没有判断环的：

FixedFixed CodeCode：100%
#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;
const int MAXN = 1e4 + 5;
const int MAXM = 1e5 + 5;
const int Mod = 1e9;
struct Edge {
    int v, next;
};
Edge edge[MAXM];

int head[MAXN], cnt;
int n, m, f[MAXN];

bool flag, vis[MAXM];

inline void AddEdge (int u, int v) {
    cnt++;
    edge[cnt].v = v;
    edge[cnt].next = head[u];
    head[u] = cnt;
    return;
}

void dfs_sum (int u, int fa) {
    if (u == 2) {
        f[fa] += f[u];
        if (f[fa] >= Mod) {
            flag = true;
            f[fa] %= Mod;
        }
        return;
    }
    
    for (int i = head[u]; i != 0; i = edge[i].next) {
        int v = edge[i].v;
        if (v == -1 || vis[i]) {
            continue;
        }
        
        vis[i] = true;
        dfs_sum (v, u);
    }
    f[fa] += f[u];
    if (f[fa] >= Mod) {
        flag = true;
        f[fa] %= Mod;
    }
    return;
}

int main() {
    scanf ("%d%d", &n, &m);
    for (int i = 1; i <= m; i++) {
        int u, v;
        scanf ("%d%d", &u, &v);
        AddEdge (u, v);
    }
    
    flag = false;
    f[2] = 1;
    dfs_sum (1, 0);
    
    if (flag) {
        int len = 0, t = f[1];
        while (t > 0) {
            t /= 10;
            len++;
        }
        for (int i = 1; i <= 9 - len; i++) {
            printf ("0");
        }
    }
    printf ("%d\n", f[1]);
    return 0;
}

后面想了想，我真的是菜的不知道怎么直接用搜索搜出环 qwq

唯一我想出来的方法是，用 tarjantarjan 把所有环缩成一个点，然后如果在到 2 的路径中经过了这个缩点，就可以判断为 inf 。

使用社交账号登录

  • Loading...
  • Loading...
  • Loading...
  • Loading...
  • Loading...